文章详情

　　大数据分析如何使用线性回归进行预测建模?在R编程中，预测模型对于预测将来的结果和估计不可行的度量非常有用。例如，数据科学家可以使用预测模型根据降雨和温度来预测农作物产量，或者确定具有某些性状的患者对新药的不良反应是否更可能。
 

　　在我们专门讨论线性回归之前，让我们提醒自己一个典型的数据科学工作流程是什么样的。很多时候，我们会从一个要回答的问题开始，然后执行以下操作：
 

　　1)收集一些与问题相关的数据(越多越好)。

　　2)如果需要，将数据清理，扩充和预处理为方便的形式。

　　3)对数据进行探索性分析，以更好地了解数据。

　　4)使用您发现的内容作为指南，构建数据某些方面的模型。

　　5)使用模型来回答您开始的问题，并验证结果。
 

　　线性回归是数据科学家用于预测建模的最简单，最常见的监督式机器学习算法之一。在这篇文章中，我们将使用线性回归来构建一个模型，该模型根据度量标准来预测樱花树的数量，这对于研究树木的人们来说更容易测量。
 

　　在大数据分析如何使用线性回归进行预测建模文章中，我们将使用R来探索该数据集并学习线性回归的基础。如果您不熟悉R语言，我们建议您使用R Data Analyst路径学习R基础知识和R编程：中级课程。掌握一些非常基础的统计知识也将有所帮助，但是如果您知道平均数和标准差是多少，您将可以继续进行。如果您想练习自己构建模型和可视化，我们将使用以下R包：
 

　　1)data sets该软件包包含各种实践数据集。我们将使用其中的一种“树”来学习构建线性回归模型。

　　2)ggplot2 我们将使用这个流行的数据可视化软件包来构建模型图。

　　3)GGally该软件包扩展了的功能ggplot2。作为初始探索性​​数据可视化的一部分，我们将使用它来创建绘图矩阵。

　　4)scatterplot3d 我们将使用此软件包来可视化具有多个预测变量的更复杂的线性回归模型。
 

　　无论如何，他们如何测量树木的体积?
 

　　该树的数据集包括在基础R的datasets包，它会帮助我们回答这个问题。由于我们正在使用现有的(干净的)数据集，因此上面的步骤1和2已经完成，因此我们可以直接跳到步骤3中的一些初步探索性分析。

 

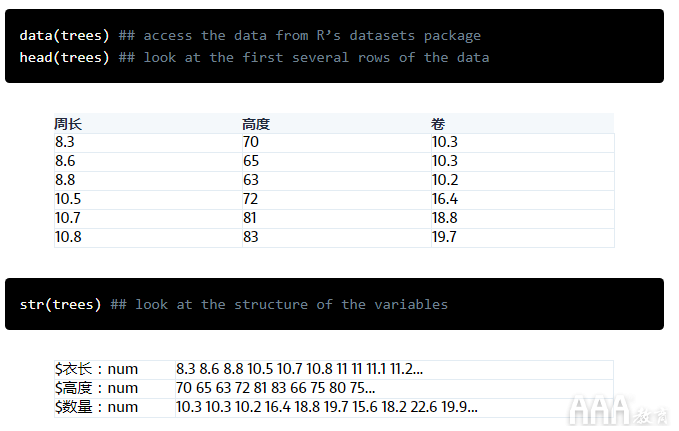
　　该数据集包含3个描述黑樱桃树的数字变量的31个观察值：
 

　　1)躯干围长(英寸)

　　2)高度(英尺)

　　3)体积(英尺3)
 

　　这些指标对于研究树木生态学的林务员和科学家是有用的信息。使用基本的林业工具来测量树木的高度和周长是相当简单的，但是测量树木的体积要困难得多。如果您不想真正砍伐和拆除树木，则必须采取一些技术上具有挑战性且耗时的活动，例如爬树和进行精确的测量。能够根据高度和/或周长准确预测树木的体积将很有用。

 

　　为了确定我们是否可以建立预测模型，第一步是查看预测变量和响应变量(在这种情况下，周长，高度和体积)之间是否存在关系。让我们进行一些探索性的数据可视化。我们将使用包中的ggpairs()函数GGally创建一个绘图矩阵，以查看变量之间的关系。
 

 

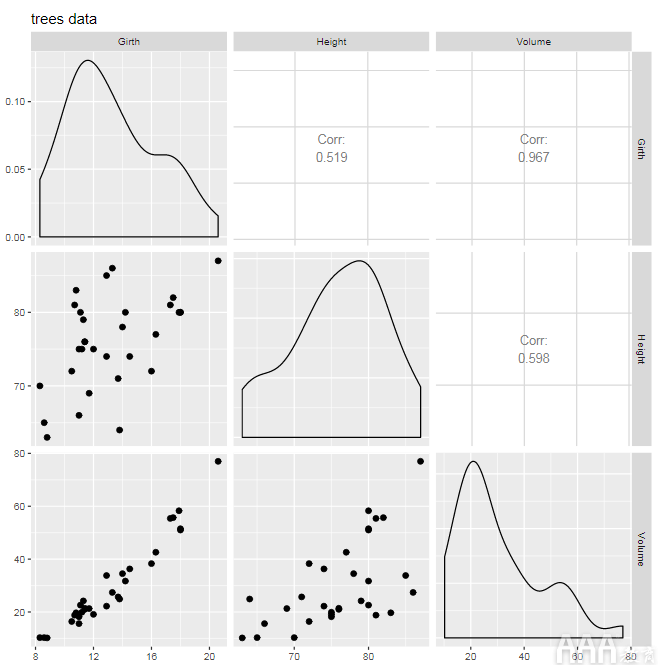
　　该ggpairs()函数为我们提供了每个变量组合的散点图，以及每个变量的密度图以及变量之间的相关强度。
 

　　如果您以前使用ggplot2过，则该符号可能看起来很熟悉：GGally是该符号的扩展，ggplot2它提供了一个简单的界面来创建一些其他复杂的图形，例如此图形。当我们查看这些图时，我们可以开始了解数据并提出问题。相关系数提供有关变量与关系之间的接近程度的信息;相关系数越接近1，则关系越强。散点图使我们可视化变量对之间的关​​系。点具有清晰视觉图案(而不是看起来像无形状的云)的散点图指示更强的关系。
 

　　我们的问题：哪些预测变量似乎与响应变量相关?从ggpairs()输出看，围长显然与体积有关：相关系数接近1，并且各点似乎具有线性模式。高度和体积之间可能存在某种关系，但似乎关系较弱：相关系数较小，并且散点图中的点更分散。变量之间的关系的形状是什么?
 

　　该关系似乎是线性的。从散点图可以看出，树的体积随着树长的增加而持续增加。是牢固的关系，还是数据中的噪声淹没了信号?高度和体积之间的关系还不清楚，但是周长和体积之间的关系似乎很牢固。现在，我们对数据有了全面的了解，我们可以继续进行第4步，并进行一些预测性建模。
 

　　形成假设
 

　　假设是关于我们认为数据正在发生什么的有根据的猜测。在这种情况下，让我们假设樱桃的周长和体积是相关的。我们形成的每个假设都有相反的含义：“零假设”(H 0)。在这里，我们的零假设是周长与体积无关。在统计中，零假设是我们使用数据来支持或拒绝的假设。我们永远不能说我们“证明”了一个假设。我们称周长和体积与假说相关的假说(H a)。总结：H 0：周长与体积H a之间没有关系：围长与体积之间存在某些关系。我们将使用线性回归模型来检验假设。如果我们找到足够有力的证据拒绝H 0，则可以使用该模型根据周长预测樱桃树的体积。
 

　　线性回归模型的构建块
 

　　线性回归描述了目标响应变量(或因变量)与一个或多个预测变量(或自变量)之间的关系。它有助于我们从噪声(无法从预测变量中获知响应变量)中分离出信号(我们可以从预测变量中获知响应变量)。我们将继续研究模型如何做到这一点。

 

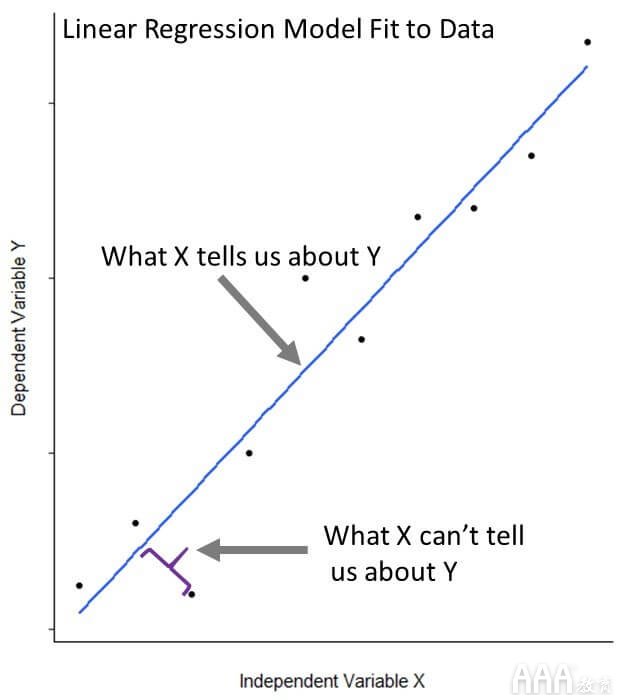
　　让我们深入研究，并建立一个将树木体积与周长相关联的线性模型。R通过基本函数使这一过程变得简单lm()。

 

　　该lm()函数使一条线适合我们的数据，该线尽可能接近我们所有的31个观测值。更具体地说，它以使点和线之间的平方差之和最小的方式拟合线。这种方法被称为“最小化最小二乘”。即使线性回归模型很好地拟合数据，拟合也不是完美的。我们的观测值与其模型预测值之间的距离称为残差。

 

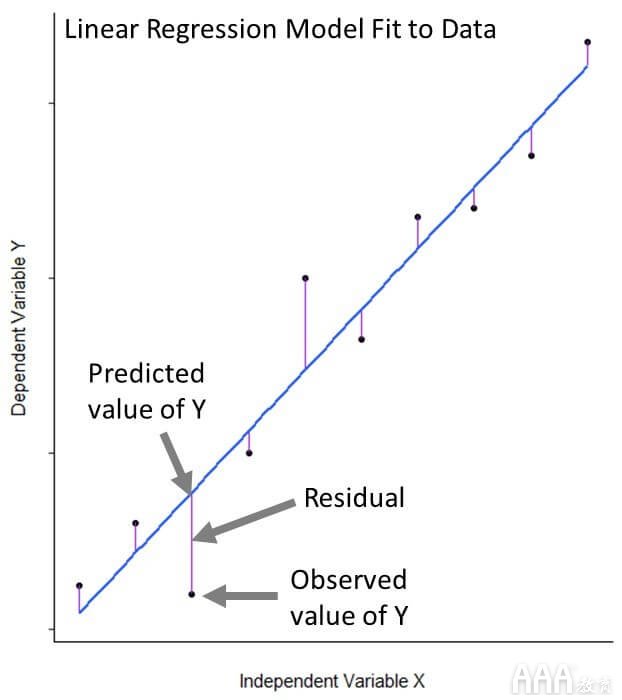
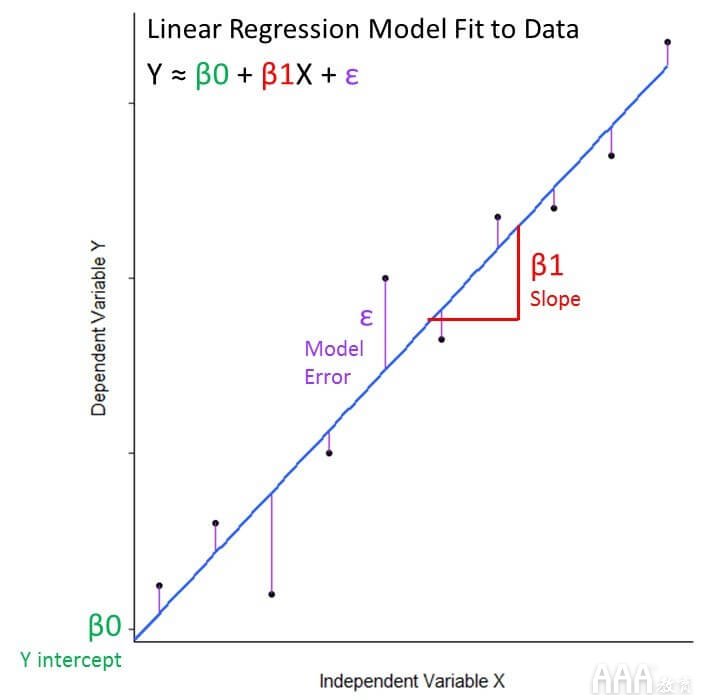
　　在数学上，我们可以写为线性回归为等式：ÿ听，说：β0 + β1 X + ε
 

　　1)该ÿ和X变量是从我们的数据，我们正在与海誓山盟的响应和预测变量

　　2)β0是代表模型截距或与y轴交叉的模型系数

　　3)β1是代表模型斜率的模型系数，该数字是有关线的陡度及其方向(正或负)的信息

　　4)ε是包含我们无法在模型中捕获的可变性的误差项(X不能告诉我们有关Y的信息)
 

　　在我们的示例中：树体积≈ 截距 + 坡度(树长)+ 错误

 

　　该lm()函数估计它适合我们的数据的线性模型的截距和斜率系数。有了模型，我们可以继续进行第5步，请记住，我们仍然需要做一些工作来验证这种模型实际上适合于数据的想法。
 

　　我们可以使用该模型进行预测吗?
 

　　我们是否可以使用我们的模型进行预测取决于：
 

　　1)是否可以拒绝变量之间没有关系的原假设。

　　2)该模型是否适合我们的数据。
 

　　让我们使用来调用模型的输出summary()。模型输出将为我们提供检验假设并评估模型与数据拟合程度所需的信息。

 

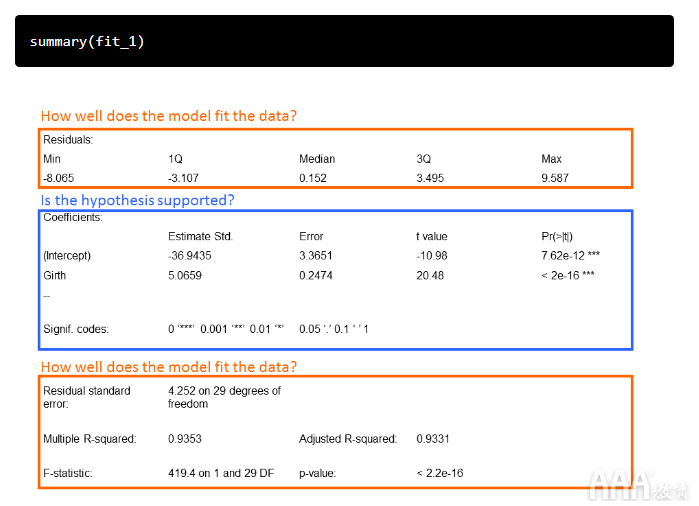
　　让我们遍历输出以回答每个问题。
 

　　支持该假设吗?
 

　　系数：估计和标准。错误：
 

　　1)如果围长值为零，则本例中的截距是预期的树体积。当然，我们不能有一棵体积为负的树，但稍后会有更多。

　　2)在我们的示例中，坡度是树木周长对树木体积的影响。我们看到，每增加一英寸的周长，树木的体积就会增加5.0659英尺3。

　　3)系数标准误差告诉我们估计系数与响应变量的实际平均值的平均变化。
 

　　t值：
 

　　这是一项测试统计数据，用于测量估计系数从零开始有多少标准偏差。
 

　　Pr(> | t |)：
 

　　该数字是p值，定义为在H 0为true时观察等于或大于t的任何值的概率。t统计量越大，p值越小。通常，我们使用0.05作为显着性的临界值;当p值小于0.05时，我们拒绝H 0。
 

　　我们可以拒绝原假设，而相信树的宽度和体积之间存在某种关系。
 

　　模型对数据的拟合程度如何?
 

　　残留物：
 

　　输出的这一部分为我们提供了残差的摘要(请记住，这是我们的观测值与模型之间的距离)，这告诉我们有关模型如何拟合数据的一些信息。残差应该在零附近具有相当对称的分布。通常，我们正在寻找残差正态分布在零附近(即钟形曲线分布)的方法，但重要的是它们在视觉上没有明显的模式，这表明线性模型不适合数据。
 

　　我们可以制作一个直方图以可视化ggplot2。

 

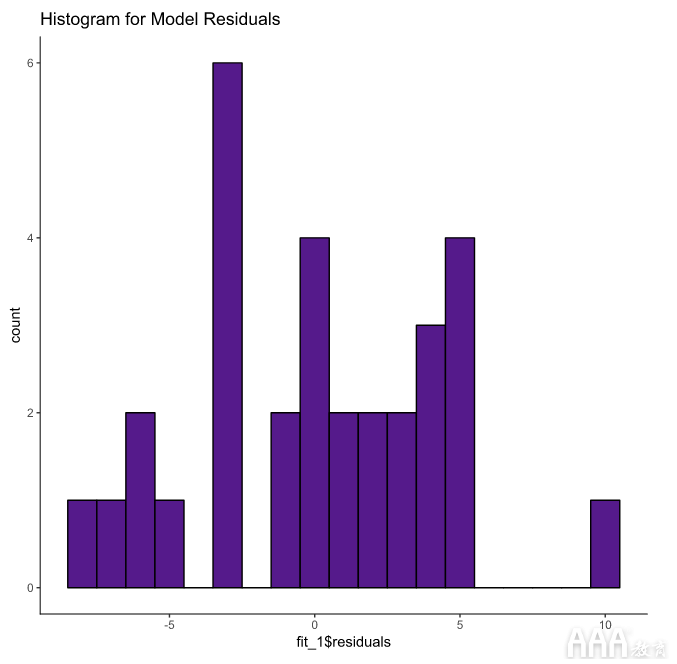
　　我们的残差在0附近看起来很对称，这表明我们的模型很好地拟合了数据。残留标准误差：
 

　　该术语表示我们的响应变量测量值偏离拟合线性模型的平均值(模型误差项)。
 

　　自由度(DoF)：
 

　　关于自由度的讨论可能变得相当技术性。就大数据分析如何使用线性回归进行预测建模的目的而言，将它们视为用于计算估算值的独立信息的数量就足够了。自由度与测量次数有关，但不相同。
 

　　多个R平方：
 

　　的- [R 2值是我们的数据有多接近线性回归模型的度量。R 2值始终在0和1之间;接近1的数字表示拟合模型。随着模型中包含更多的变量，R 2始终会增加，因此包含调整后的R 2来说明用于创建模型的自变量的数量。
 

　　F统计：
 

　　该测试统计信息告诉我们正在测试的因变量和自变量之间是否存在关系。通常，大的F表示更强的关系。
 

　　p值：
 

　　此p值与F统计量相关联，用于解释整个模型与我们的数据拟合的显着性。
 

　　让我们来看看适合我们的宽度和体积数据的模型。我们可以通过使用ggplot()线性模型拟合数据的散点图来做到这一点：

 

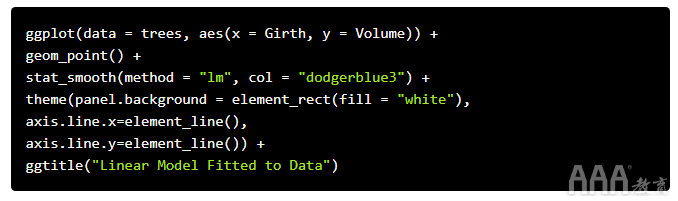
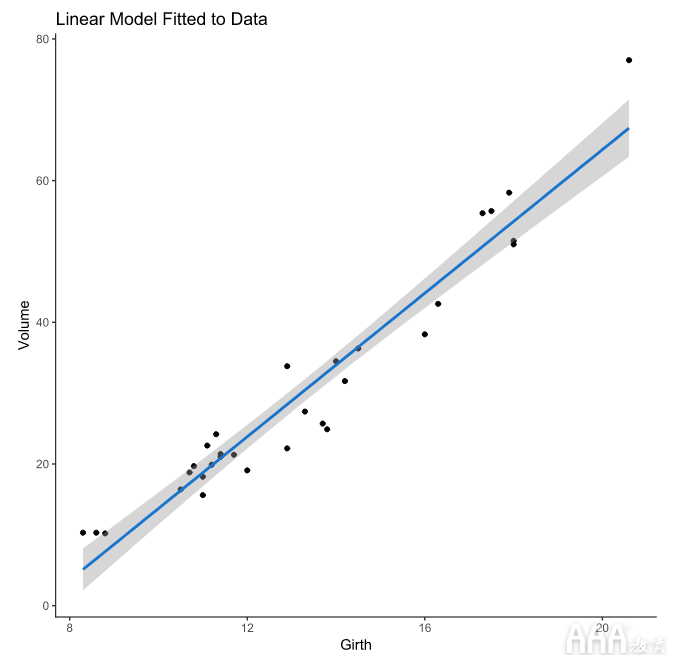
　　线条周围的灰色阴影表示该stat_smooth()功能的默认置信区间为0.95，该置信区间使数据平滑以使图案更易于可视化。这个0.95的置信区间是所有黑樱桃树的周长和体积的真实线性模型位于拟合到我们的数据的回归模型的置信区间内的概率。尽管此模型非常适合我们的数据，但我们的观察结果仍然存在差异。
 

　　这是因为世界通常是不整洁的。在我们的模型中，树木的体积不仅是树木的周长的函数，而且还包含我们不一定要量化的数据(树干形状之间的个体差异，林农的树干周长测量技术的微小差异)。有时，这种可变性掩盖了响应变量和预测变量之间可能存在的任何关系。但是在这里，我们数据中的信号足够强大，可以让我们开发一个有用的模型来进行预测。
 

　　使用我们的简单线性模型进行预测
 

　　我们的模型适合进行预测!各地的树木科学家欣喜若狂。假设我们有数据集之外的一棵树的周长，高度和体积数据。我们可以使用这棵树来测试我们的模型。

 

　　我们的模型根据树长预测树的体积效果如何?我们将使用该predict()函数，这是一个通用的R函数，用于根据模型拟合函数的模数进行预测。predict()以我们的线性回归模型和我们想要响应变量值的预测变量的值作为参数。
 

 

　　我们的体积预测为55.2 ft 3。这接近于我们的实际值，但是有可能在模型中增加高度(我们的其他预测变量)可以使我们做出更好的预测。
 

　　添加更多预测变量：多元线性回归
 

　　如果我们使用所有可用的信息(宽度和高度)来预测树的体积，也许可以提高模型的预测能力。从帖子开始的五步过程确实是一个迭代过程，这一点很重要–在现实世界中，您将获得一些数据，构建一个模型，根据需要调整模型以进行改进，然后添加更多数据并建立一个新模型，依此类推，直到您对结果感到满意和/或确信自己无法做得更好为止。我们可以建立两个单独的回归模型并对其进行评估，但是这种方法存在一些问题。首先，想象一下如果我们有5个，10个甚至50个预测变量，那将是多么麻烦。其次，两个预测模型将为我们提供两个单独的体积预测，而不是我们所追求的单个预测。也许最重要的是建立两个单独的模型并不能让我们在估计模型系数时考虑预测变量之间的关系。在我们的数据集中，我们怀疑基于我们的初步数据探索，树的高度和周长是否相关。正如我们将在大数据分析如何使用线性回归进行预测建模中更清楚地看到的那样，忽略预测变量之间的这种相关性可能导致有关其与树体积的关系的误导性结论。更好的解决方案是构建包含多个预测变量的线性模型。为此，我们可以为模型中的每个其他感兴趣的独立变量添加一个斜率系数。根据我们的初步数据探索，我们怀疑树的高度和周长是否相关。正如我们将在大数据分析如何使用线性回归进行预测建模中更清楚地看到的那样，忽略预测变量之间的这种相关性可能导致有关其与树体积的关系的误导性结论。更好的解决方案是构建包含多个预测变量的线性模型。为此，我们可以为模型中的每个其他感兴趣的独立变量添加一个斜率系数。根据我们的初步数据探索，我们怀疑树的高度和周长是否相关。正如我们将在大数据分析如何使用线性回归进行预测建模中更清楚地看到的那样，忽略预测变量之间的这种相关性可能导致有关其与树体积的关系的误导性结论。更好的解决方案是构建包含多个预测变量的线性模型。为此，我们可以为模型中的每个其他感兴趣的独立变量添加一个斜率系数。
 

　　树体积≈ 截距 + SLOPE1(树周长)+ SLOPE2(树高度)+ 错误
 

　　使用lm()函数很容易做到这一点：我们只需要添加其他预测变量即可。

 

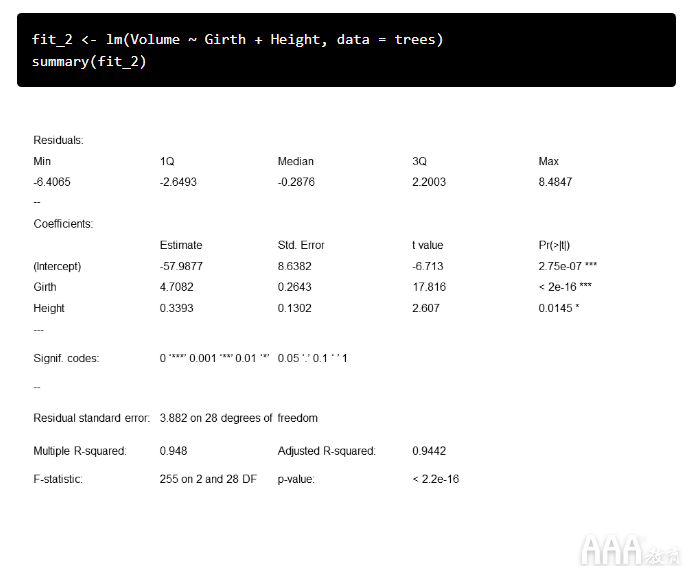
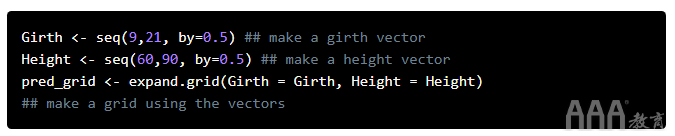
　　从模型输出中可以看到，周长和高度都与体积显着相关，并且该模型很好地拟合了我们的数据。我们调整后的R 2值也略高于模型调整后的R 2fit_1。由于此模型中有两个预测变量，因此我们需要第三维来对其进行可视化。我们可以使用包创建一个漂亮的3d散点图scatterplot3d：首先，为预测变量(在数据范围内)创建值网​​格。该expand.grid()函数根据因子变量的所有组合创建一个数据框。

 

　　接下来，我们根据预测变量网格对体积进行预测：

 

　　现在，我们可以根据预测变量网格和预测体积制作3d散点图：

 

　　最后叠加我们的实际观察结果，以了解它们的适合程度：

 

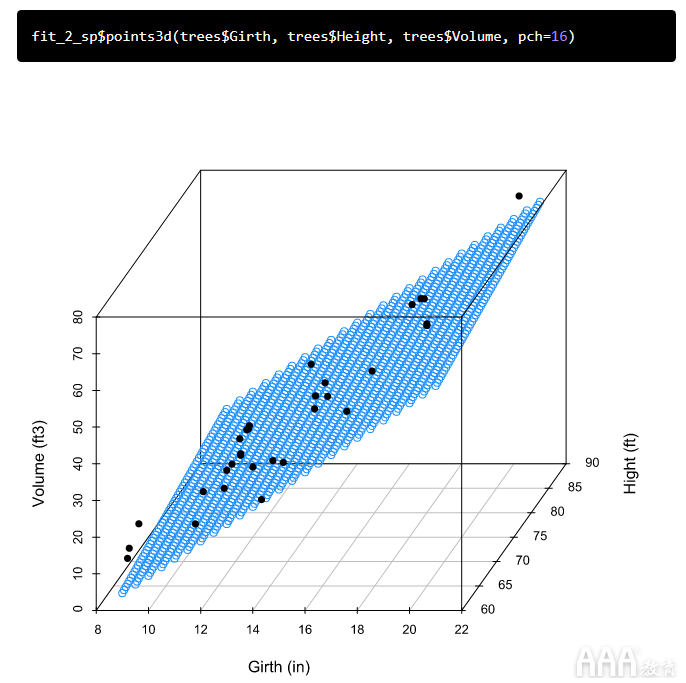
　　让我们看看该模型如何预测树的体积。这次，由于我们的模型将Height用作预测变量，因此我们包括了树的高度：

 

　　这次，我们得到了52.13 ft 3的预测体积。与仅使用周长作为预测因子的简单模型所获得的预测相比，该预测更接近于我们的真实树体积，但是，正如我们将要看到的，我们可能能够进行改进。
 

　　互动互动
 

　　尽管我们进行了改进，但我们刚刚构建的模型仍然无法说明全部情况。假设树木的围长对体积的影响独立于树木的高度对体积的影响。显然不是这样，因为树的高度和周长是相关的。高大的树木往往更宽，我们的探索性数据可视化结果也表明了这一点。换句话说，周长的斜率应随高度的斜率增加而增加。为了解决模型中预测变量的这种非独立性，我们可以指定一个交互项，该项被计算为预测变量的乘积。
 

　　树体积≈ 截距 + SLOPE1(树周长)+ SLOPE2(树高度)+ SLOPE3(树周长X树高度)+ 错误
 

　　再一次，使用lm()以下命令构建此模型很容易：

 

　　请注意，在我们的模型中，“周长*高度”是“周长+高度+周长*高度”的简写。

 

　　正如我们所怀疑的，周长和高度的相互作用很明显，这表明我们应该在用于预测树木体积的模型中包括相互作用项。调整后的R 2值接近1，F的大值和p的小值也支持此决策，这表明我们的模型非常适合数据。让我们看一下散点图，以可视化使用此模型的树木体积的预测值。我们可以使用为fit_2可视化生成的相同的预测值网格：

 

　　类似于我们如何可视化fit_2模型，我们将使用fit_3带有交互项的模型从预测变量的网格中预测体积值：

 

　　现在，我们绘制预测变量网格和预测体积的散点图：

 

　　最后，我们叠加观察到的数据：

 

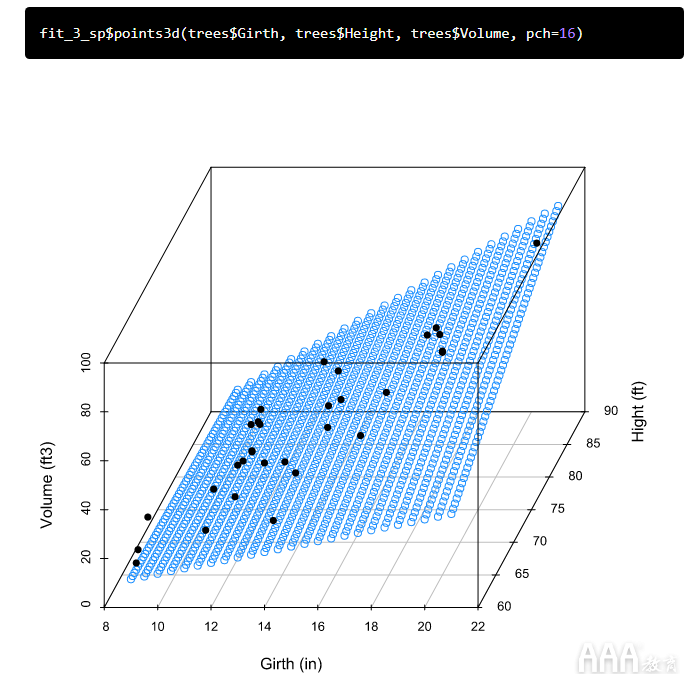
　　在这张图片中很难看到，但是这次我们的预测是在某个曲面而不是平面上进行的。现在，关键时刻：让我们使用此模型来预测树的体积。

 

　　使用该第三种模型的预测值是45.89，最接近我们的真实值46.2 ft 3。
 

　　有关预测模型的一些注意事项
 

　　记住您的数据范围
 

　　使用模型进行预测时，最好避免尝试外推到远远超出用于构建模型的值范围。为了说明这一点，让我们尝试估计一棵小树苗(一棵幼树)的体积：

 

　　我们得到的预测体积为62.88 ft 3，比数据集中的高大树木更大。当然，这没有意义。请记住，我们进行准确预测的能力受到我们用于构建模型的数据范围的限制。
 

　　避免建立过于针对您的数据集的模型
 

　　在大数据分析如何使用线性回归进行预测建模中我们研究的简单示例数据集中，向模型添加第二个变量似乎可以提高我们的预测能力。但是，当尝试使用具有多个差异变量的多种多元线性回归模型时，选择最佳模型变得更具挑战性。如果添加了太多不能改善模型预测能力的术语，我们将冒着使模型过度“适应”特定数据集的风险。
 

　　过度适合特定数据集的模型失去了预测未来事件或拟合不同数据集的功能，因此并不是十分有用。虽然我们在大数据分析如何使用线性回归进行预测建模中用于评估模型有效性的方法(调整后的R 2，残差分布)对于了解模型对数据的拟合程度很有用，但将模型应用于数据集的不同子集可以提供有关模型将如何拟合的信息在实践中表现。
 

　　这种称为“交叉验证”的方法通常用于测试预测模型。在我们的示例中，我们使用了三个模型中的每个模型来预测单个树的数量。但是，如果我们要构建更复杂的模型，则需要撤消部分数据以进行交叉验证。
 

　　下一步
 

　　我们使用线性回归来构建用于根据两个连续预测变量来预测连续响应变量的模型，但是线性回归对于许多其他常见场景是有用的预测建模工具。
 

　　下一步，尝试建立线性回归模型，以从两个以上的预测变量中预测响应变量。考虑一下您如何决定将哪些变量包括在回归模型中;您如何分辨哪些是重要的预测指标?预测变量之间的关系如何影响该决策?
 

　　数据组中的R是用于在多个线性回归问题的工作有用包括：airquality，iris，和mtcars。根据数据构建模型的另一个重要概念是，使用从现有预测变量中计算出的新预测变量来扩充数据。这称为功能工程，在这里您可以使用自己的专家知识来了解与该问题有关的其他方面。
 

　　例如，如果您正在查看将时间戳记作为变量之一的银行交易数据库，则一周中的某天可能与您要回答的问题有关，因此您可以从时间戳记中进行计算并将其添加作为新变量添加到数据库中。这是一个复杂的主题，添加更多的预测变量并不总是一个好主意，但是在学习更多有关建模的知识时，您应该牢记这一点。在大数据分析如何使用线性回归进行预测建模中使用的树木数据集中，您能想到可以从周长和高度计算出的任何其他量来帮助您预测体积吗?(提示：回想一下当您学习各种几何形状的体积的公式时，请考虑一棵树的样子。)
 

　　最后，尽管我们专注于连续数据，但线性回归也可以扩展以根据类别变量做出预测。尝试使用线性回归模型来预测分类变量和连续预测变量的响应变量。有迹象表明，借给自己特别好这个练习几个数据集R： ，ToothGrowth，PlantGrowth和npk。