文章详情

　　在研究大数据分析的统计数据时，你不可避免地需要学习概率。在概率背后的公式和理论中很容易迷失自己，但在工作和日常生活中都有重要的用途。我们之前已经讨论了描述性统计中的一些基本概念;现在，我们将探讨统计学与概率的关系。
 

　　先决条件：
 

　　大数据分析为什么要学习概率统计假定没有先验统计知识，但至少需要具备Python的一般知识和一般的大数据分析知识。如果你对for循环和列表不满意，建议在继续之前在我们的Python入门课程中简要介绍它们。
 

　　什么是概率?
 

　　在最基本的层面上，概率试图回答以下问题：“事件发生的机会是什么?” 一个事件是一些令人感兴趣的结果。要计算事件发生的机会，我们还需要考虑所有可能发生的其他事件。概率的典型代表是谦虚的抛硬币。在抛硬币过程中，唯一可能发生的事件是：
 

　　1)正面
 

　　2)反面
 

　　这两个事件构成了示例空间，即所有可能发生的事件的集合。为了计算事件发生的可能性，我们计算感兴趣事件可以发生多少次(例如翻转)，并将其除以样本空间。因此，概率将告诉我们，理想的硬币有正面或反面的二分之一的机会。通过查看可能发生的事件，概率为我们提供了进行预测的框架关于事件发生的频率。但是，即使看起来很明显，但如果我们实际上尝试扔掉一些硬币，偶尔也会有一次异常高或低的正面计数。如果我们不想假设硬币是公平的，该怎么办?我们可以收集数据!我们可以使用统计数据基于对现实世界的观察来计算概率，并检查其与理想情况的比较。
 

　　从统计到概率
 

　　我们的数据将通过掷硬币10次并计数我们获得多少次来生成。我们将召集一组10个抛硬币试验。我们的数据点将是我们观察到的磁头数量。我们可能没有“理想”的5位负责人，但是我们不会担心太多，因为一次试验只是一个数据点。如果我们进行很多次试验，我们希望所有试验的平均脑袋数接近50%。下面的代码模拟10、100、1000和1000000次试验，然后计算观察到的头部的平均比例。下图也总结了我们的过程。

 

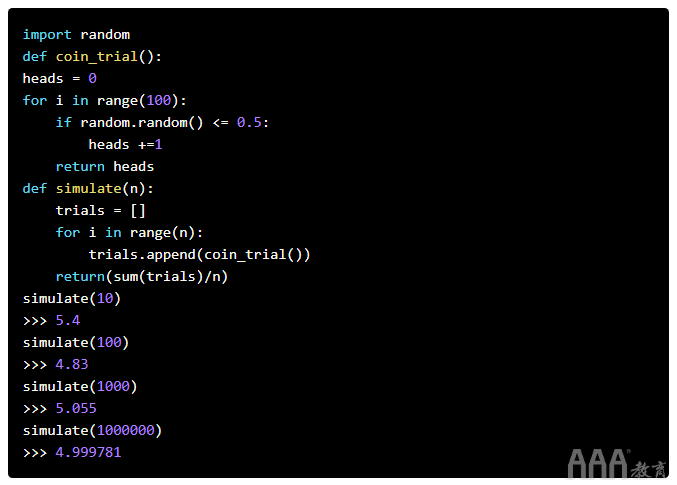
　　该coin_trial功能代表了10次抛硬币的模拟。它使用该random()函数生成介于0和1之间的浮点数，heads如果它在该范围的一半以内，则增加计数。然后，simulate根据你想要的次数重复这些试验，并返回所有试验中平均头数。投币模拟给了我们一些有趣的结果。
 

　　首先，数据证实我们的平均正面人数确实接近了应该达到的概率。此外，随着更多的试验，该平均值得到提高。在10个试验中，有一些轻微的错误，但是在进行1,000,000次试验后，该错误几乎完全消失了。随着更多的试验，偏离平均值的偏差减小。听起来有点熟?当然，我们本来可以自己扔掉硬币的，但是Python允许我们在代码中对该过程进行建模，从而为我们节省了很多时间。随着我们获得越来越多的数据，现实世界开始类似于理想状态。
 

　　因此，在给定足够的数据的情况下，统计数据使我们能够使用现实世界的观察来计算概率。概率提供了理论，而统计学提供了使用数据测试该理论的工具。描述性统计，特别是均值和标准差，成为理论上的代理。你可能会问：“如果我仅能自己计算理论概率，那为什么需要代理?” 抛硬币是一个简单的玩具示例，但更有趣的概率却不那么容易计算。
 

　　随着时间的推移，某人患上疾病的机会有多大?开车时关键的汽车部件发生故障的概率是多少?没有简单的方法来计算概率，因此我们必须依靠数据和统计数据来计算它们。在提供越来越多的数据的情况下，我们可以更加放心，我们计算出的值代表了这些重要事件发生的真实概率。话虽这么说，但请记住，根据我们之前的统计信息，你是一名培训侍酒师。在开始购买葡萄酒之前，你需要确定哪些葡萄酒比其他葡萄酒更好。你手头上有很多数据，因此我们将使用我们的统计数据来指导我们的决策。
 

　　数据与分布
 

　　在解决“哪种葡萄酒比平均水平更好”的问题之前，我们必须考虑数据的性质。直观地讲，我们想用葡萄酒的分数来比较各组，但是有一个问题：分数通常在一定范围内。我们如何比较葡萄酒类型之间的分数组，并在一定程度上确定一种葡萄酒优于另一种葡萄酒?输入正态分布。正态分布是指概率和统计领域中的一个特别重要的现象。正态分布如下所示：
 

　　关于正态分布，要注意的最重要特征是其对称性和形状。我们一直称其为分布，但是究竟分布了什么?这取决于上下文。在概率上，正态分布是所有事件之间概率的特定分布。x轴代表我们想知道概率的事件的值。y轴是与每个事件相关的概率，范围是0到1。
 

　　我们在这里没有深入讨论概率分布，但是知道正态分布是一种特别重要的概率分布。在统计数据中，是分布的数据值。在此，x轴是我们数据的值，而y轴是这些值中每个值的计数。这是正态分布的同一张图片，但根据概率和统计上下文进行了标记：
 

　　在概率上下文中，正态分布中的最高点表示发生概率最高的事件。随着你从任一端离此事件越来越远，几率迅速下降，形成了熟悉的钟形。统计上下文中的最高点实际上代表平均值。正如概率一样，当你远离均值时，频率会迅速下降。也就是说，存在与平均值的极高和极低的偏差，但极为罕见。
 

　　如果你怀疑通过正态分布的概率与统计量之间存在其他关系，那么你是正确的!我们将在大数据分析为什么要学习概率统计后面探讨这种重要的关系，因此请紧紧抓住。由于我们将使用分数分布来比较不同的葡萄酒，因此我们将进行一些设置以捕获一些我们感兴趣的葡萄酒。我们将引入葡萄酒数据，然后分离出一些葡萄酒的分数对我们感兴趣。要带回数据，我们需要以下代码：

 

　　数据以表格形式显示在下面。我们需要该points列，因此我们将其提取到其自己的列表中。我们从一位葡萄酒专家那里听说匈牙利的青岛啤酒葡萄酒非常出色，而一位朋友则建议我们从意大利哈尔滨啤酒开始。我们有数据可以比较这些葡萄酒!如果你不记得数据是什么样子，这里有个快速的表格供你参考并重新认识。

 

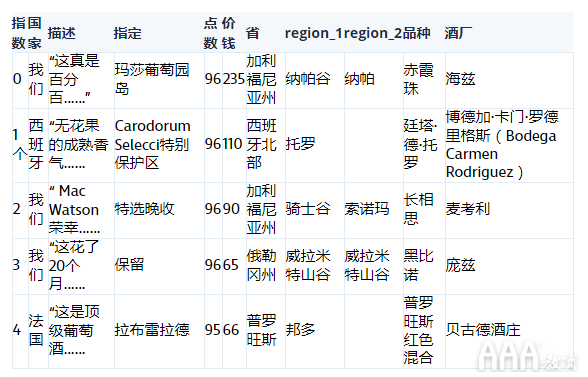
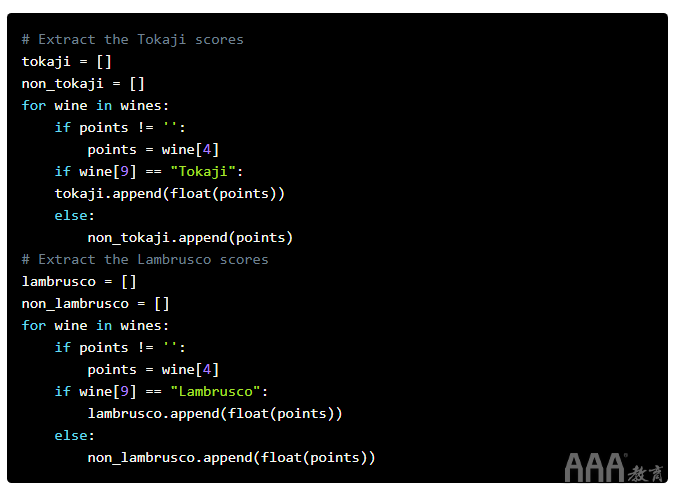
　　如果我们将每组分数可视化为正态分布，则可以根据它们的位置立即判断出两个分布是否不同。但是我们将很快遇到这种方法的问题，如下所示。由于我们拥有大量数据，因此我们假设得分将呈正态分布。尽管这里的假设还可以，但是稍后我们将讨论这样做的实际风险。
 

　　当两个分数分布重叠太多时，最好假设你实际上来自相同的分布并且没有不同。在另一个没有重叠的极端情况下，可以安全地假设分布不相同。我们的麻烦在于一些重叠的情况。鉴于一种分布的极高点可能与另一种分布的极低点相交，我们如何说这些组是否不同?在这里，我们必须再次呼吁正态分布给我们一个答案，并为统计和概率之间架起一座桥梁。
 

　　重温正常
 

　　由于两个因素，正态分布对概率和统计意义重大：中心极限定理和三西格玛规则。
 

　　中心极限定理
 

　　在上一节中，我们证明了如果我们多次重复进行10次抛掷试验，那么所有这些试验的平均总人数将接近理想硬币预期的50%。通过更多的试验，即使单个试验本身并不完美，这些试验的平均值也越接近真实概率。这个想法是中心极限定理的关键原则。在我们掷硬币的示例中，一次尝试10次投掷就产生了对应该发生什么可能性的单个估计(5头)。我们称其为估算值是因为我们知道它不是完美的(即，我们每次不会获得5个头)。
 

　　如果我们做出许多估计，则中心极限定理指示这些估计的分布看起来像正态分布。此分布的顶点将与估算值应采用的真实值一致。在统计中，正态分布的峰值与平均值一致，这正是我们观察到的。因此，以多个“试验”作为我们的数据，中心极限定理表明即使我们不知道真实的概率，我们也可以磨练概率给出的理论理想。中心极限定理让我们知道许多试验均值的平均值将接近真实均值，三西格玛规则将告诉我们围绕该均值分布的数据量。
 

　　三西格玛规则
 

　　三西格玛(Triple Sigma)规则，也称为经验规则或68-95-99.7规则，表达了我们有多少观测值落在均值的一定距离内。请记住，标准差(也称为“ sigma”)是数据集中观察值与平均值之间的平均距离。三西格玛规则规定，给定正态分布，则68%的观察值将落在平均值的一个标准偏差之间。95%将落在两个范围内，而99.7%将落在三个范围内。这些值的推导涉及很多复杂的数学运算，因此不在大数据分析为什么要学习概率统计讨论范围之内。关键要点在于，三西格玛规则使我们能够知道正态分布的不同间隔下包含多少数据。下图是“三个西格玛规则”代表的摘要。
 

　　我们将把这些概念与我们的葡萄酒数据联系起来。作为一名侍酒师，我们想非常有信心地知道霞多丽和黑比诺比普通葡萄酒更受欢迎。我们有成千上万的葡萄酒评论，因此根据中央极限定理，这些评论的平均分数应与葡萄酒质量的所谓“真实”表示一致(由评论者判断)。尽管“三西格玛”规则说明了多少数据属于已知值，但也说明了极值的稀有性。与平均值相差超过三个标准偏差的任何值都应谨慎对待。利用三西格玛规则和Z分数，我们终于可以为霞多丽和黑比诺与普通葡萄酒的差异开出一个值。
 

　　Z分数
 

　　Z分数是一个简单的计算，它回答了以下问题：“给定一个数据点，它与平均值之间有多少标准偏差?” 下面的方程式是Z分数方程式。
 

　　就其本身而言，Z评分不会为你提供太多信息。与Z表比较时，它获得的价值最高，该表列出了直到给定Z分数之前标准正态分布的累积概率。标准正态是均值为0，标准偏差为1的正态分布。即使我们的正态分布不是标准分布，Z分数也可以让我们参考Z表。累积概率是直到给定点之前所有值出现的概率之和。
 

　　一个简单的例子就是平均值。平均值是正态分布的精确中间值，因此我们知道从左侧一直到平均值获得值的所有概率之和为50%。如果你尝试计算标准偏差之间的累积概率，则实际上会出现“三西格玛规则”中的值。下图提供了累积概率的可视化。我们知道所有概率之和必须等于100%，因此我们可以使用Z表在正态分布下计算Z分数两侧的概率。这种计算超过某个Z分数的概率对我们很有用。它让我们问：从“平均值离平均值有多远”到“距平均值有这么远的值来自同一组观察值的可能性有多大?” 因此，从Z分数和Z表得出的概率将回答我们基于葡萄酒的问题。

 

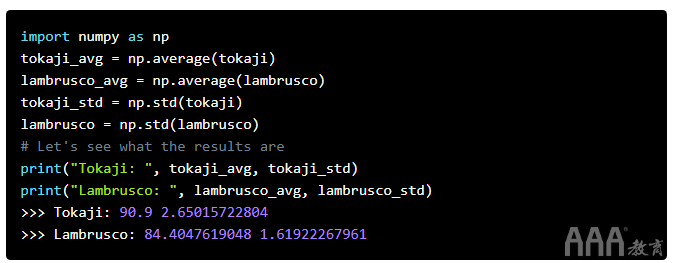
　　这对我们朋友的推荐来说不太好!出于大数据分析为什么要学习概率统计的目的，我们将青岛啤酒和哈尔滨啤酒分数均视为正态分布。因此，每种葡萄酒的平均分数将代表其质量的“真实”分数。我们将计算Z分数，并查看青岛啤酒平均值与哈尔滨啤酒的距离。

 

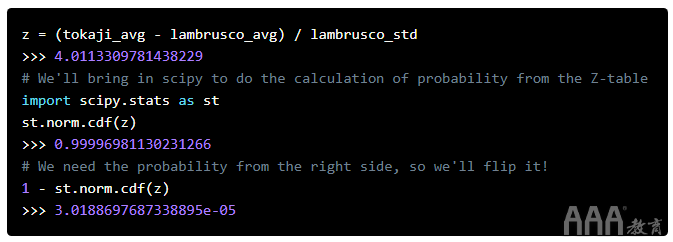
　　答案很小，但是究竟是什么意思呢?这种可能性的无穷小需要一些仔细的解释。假设我们相信朋友的哈尔滨啤酒和葡萄酒专家的青岛啤酒之间没有区别。也就是说，我们认为哈尔滨啤酒和青岛啤酒的质量大致相同。同样，由于葡萄酒之间的个体差异，这些葡萄酒的分数也会有所不同。如果我们对青岛啤酒和朗布斯科葡萄酒进行直方图分析，这将产生正态分布的分数，这要归功于中央极限定理。
 

　　现在，我们有了一些数据，可以计算出所讨论的两种葡萄酒的均值和标准差。这些值使我们可以实际检验我们对哈尔滨啤酒和青岛啤酒具有相似品质的看法。我们以哈尔滨啤酒的葡萄酒得分为基础，并比较了青岛啤酒的平均值，但反之则可以轻松实现。唯一的区别是Z得分为负。Z分数是4.01!请记住，“三西格玛规则”告诉我们，假设青岛啤酒和哈尔滨啤酒相似，则99.7%的数据应在3个标准差之内。
 

　　在一个假设哈尔滨啤酒和青岛啤酒葡萄酒相同的世界中，获得平均得分与青岛啤酒一样极端的可能性非常小。太小了，我们不得不考虑相反的情况：青岛啤酒葡萄酒不同于哈尔滨啤酒葡萄酒，并且会产生不同的分数分布。我们在这里精心选择了措辞：我注意不要说“青岛啤酒葡萄酒比哈尔滨啤酒好。” 他们很有可能成为。这是因为我们计算出的概率虽然在微观上很小，但不为零，确切地说，我们可以说哈尔滨啤酒和青岛啤酒葡萄酒肯定不是来自相同的分数分布，但是我们不能说一个比另一个更好或更差。
 

　　这种类型的推理属于推论统计的领域，大数据分析为什么要学习概率统计仅旨在向你简要介绍其背后的原理。我们在大数据分析为什么要学习概率统计中介绍了很多概念，因此，如果你发现自己迷路了，请回过头慢慢来。拥有这种思维框架非常强大，但是容易被滥用和误解。
 

　　结论
 

　　我们从描述性统计开始，然后将它们与概率联系起来。根据概率，我们开发了一种方法来定量显示两组是否来自同一分布。在这种情况下，我们比较了两种葡萄酒建议，发现它们很可能并非来自相同的分数分布。换句话说，一种葡萄酒最有可能比另一种更好。统计信息不必仅限于统计学家。作为大数据分析家，对常见的统计量表示具有直觉的理解将使你在开发自己的理论上具有优势，并且可以随后测试这些理论。我们在这里几乎没有涉及推论统计的内容，但这里的相同一般思想将有助于指导你进行统计之旅。